Yearly Archives: 2021

Ex 2.1 Class 12 Maths Question 1-10.
Find the principal values of the following:
(1) 
(2) 
(3) 
(4) 
(5) 
(6) 
(7) 
(8)
(9) 
(10) 
Solution:
(1) Let  = y
∴ 
the range of principal value of sin^-1 is

Ex 2.1 Class 12 Maths Question 11-12.
Find the principal values of the following:
(11) 
(12) 
Solution:
(11) 
Now tan^-1 (1) = 
∴the range of principal value branch of

Ex 2.1 Class 12 Maths Question 13.
If sin^-1 x = y, then
(a) 0 ≤ y ≤ π
(b) 
(c) 0 < y < π
(d) 
Solution:
The range of principal value of sin is 
∴ if sin^-1 x = y then

Option (b) is correct

Ex 2.1 Class 12 Maths Question 14.
 is equal to
(a) π
(b) 
(c) 
(d) 
Solution:

∴ Principal values of sec^-1 is [0,π] – 

Option (b) is correct

Ex 2.2 Class 12 Maths Question 1.

Solution:
Let sin^-1 x = θ
sin θ = x sin 3θ = 3 sin θ – 4 sin³ θ
sin 3θ = 3x – 4x³
3θ = sin^-1 (3x – 4x³)
or 

Ex 2.2 Class 12 Maths Question 2.

Solution:
Let cos^-1 x = θ
x = cos θ
R.H.S= cos^-1 (4x³ – 3cosx)
= cos^-1 (4 cos³θ – 3 cosθ)
= cos^-1 (cos 3θ) [∴ cos 3θ = 4 cos³ θ – 3 cos θ]
= 3θ
= 3 cos^-1 x
= L.H.S.

Ex 2.2 Class 12 Maths Question 3.

Solution:
L.H.S = 
= 
= 
= R.H.S

Ex 2.2 Class 12 Maths Question 4.

Solution:
L.H.S =

Ex 2.2 Class 12 Maths Question 5.
Write the function in the simplest form

Solution:
Putting x = θ
∴ θ = tan^-1 x

Ex 2.2 Class 12 Maths Question 6.

Solution:
Given expression

Let x = secθ

Ex 2.2 Class 12 Maths Question 7.

Solution:

= 

Ex 2.2 Class 12 Maths Question 8.

Solution:

Dividing numerator and denominator by cos x

Ex 2.2 Class 12 Maths Question 9.

Solution:
Let x = a sinθ
=>  = sinθ

Ex 2.2 Class 12 Maths Question 10.

Solution:
Put x = a tanθ,
we get

Ex 2.2 Class 12 Maths Question 11.
Find the value of the following

Solution:

= 

Ex 2.2 Class 12 Maths Question 12.
cot[tan^-1 a + cot^-1 a]
Solution:
Given
cot[tan^-1 a + cot^-1 a]
= 

Ex 2.2 Class 12 Maths Question 13.

Solution:
Putting x = tanθ
=> tan^-1 x = θ

Ex 2.2 Class 12 Maths Question 14.
If  then find the value of x
Solution:

Ex 2.2 Class 12 Maths Question 15.
If  then find the value of x
Solution:
L.H.S

Ex 2.2 Class 12 Maths Question 16.

Solution:

= 
= 

Ex 2.2 Class 12 Maths Question 17.

Solution:

= 
= 

Ex 2.2 Class 12 Maths Question 18.

Solution:

Let 
sinθ = 

Ex 2.2 Class 12 Maths Question 19.
 is equal to
(a) 
(b) 
(c) 
(d) 
Solution:

= 

Ex 2.2 Class 12 Maths Question 20.
 is equal to
(a) 
(b) 
(c) 
(d) 1
Solution:

Ex 2.2 Class 12 Maths Question 21.
 is equal to
(a) π
(b) 
(c) 0
(d) 2√3
Solution:

Ex 1.1 Class 12 Maths Question 1.
Determine whether each of the following relations are reflexive, symmetric and transitive:
(i) Relation R in the set A= {1,2,3,….13,14} defined as R={(x,y):3x – y = 0}
(ii) Relation R in the set N of natural numbers defined as R= {(x, y): y = x + 5 and x < 4}
(iii) Relation R in the set A= {1,2,3,4,5,6} as R= {(x, y): y is divisible by x}
(iv) Relation R in the set Z of all integers defined as R = {(x, y): x – y is an integer}
(v) Relation R in the set A of human beings in a town at a particular time given by
(a) R = {(x, y): x and y work at the same place}
(b) R = {(x, y) : x and y live in the same locality}
(c) R = {(x, y) : x is exactly 7 cm taller than y}
(d) R={(x,y) : x is wife of y}
(e) R= {(x, y): x is father of y}
Solution:
(i) Relation R in the set A = {1, 2,….,14} defined as R= {(x,y): 3x  -y = 0}
(a) Put y = x, 3x – x ≠ 0 => R is not reflexive.
(b) If 3x – y = 0, then 3y – x ≠ 0, R is not symmetric
(c) If 3x – y = 0, 3y – z = 0,then 3x – z ≠ 0,R is not transitive.

(ii) Relations in the set N of natural numbers in defined by R = {(x, y): y = x + 5 and x < 4}
(a) Putting y = x, x ≠ x + 5, R is not reflexive
(b) Putting y = x + 5, then x ≠ y + 5,R is not symmetric.
(c) If y = x + 5, z = y + 5, then z ≠ x + 5 =>R is not transitive.

(iii) Relation R in the set A = {1,2,3,4,5,6} asR = {(x, y): y is divisible by x}
(a) Putting y = x, x is divisible by x => R is reflexive.
(b) If y is divisible by x, then x is not divisible by y when x ≠ y => R is not symmetric.
(c) If y is divisible by x and z is divisible by y then z is divisible by x e.g., 2 is divisible by 1,4 is divisible by 2.
=> 4 is divisible by 1 => R is transitive.

(iv) Relation R in Z of all integers defined as R = {(x, y): x – y is an integer}
(a) x – x=0 is an integer => R is reflexive
(b) x – y is an integer so is y – x => R is transitive.
(c) x – y is an integer, y- z is an integer and x – z is also an integer => R is transitive.

(v) R is a set of human beings in a town at a particular time.
(a) R = {(x, y)} : x and y work at the same place. It is reflexive as x works at the same place. It is symmetric since x and y or y and x work at same place.
It is transitive since X, y work at the same place and if y, z work at the same place,u then x and z also work at the same place.
(b) R : {(x, y) : x and y line in the same locality}
With similar reasoning as in part (a), R is reflexive, symmetrical and transitive.
(c) R: {(x, y)}: x is exactly 7 cm taller than y it is not reflexive: x cannot 7 cm taller than x. It is not symmetric: x is exactly 7 cm taller than y, y cannot be exactly 7 cm taller than x. It is not transitive: If x is exactly 7 cm taller than y and if y is exactly taller than z, then x is not exactly 7 cm taller than z.
(d) R = {(x, y): x is wife of y}
R is not reflexive: x cannot be wife of x. R is not symmetric: x is wife of y but y is not wife of x.
R is not transitive: if x is a wife of y then y cannot be the wife of anybody else.
(e) R= {(x, y): x is a father of y}
It is not reflexive: x cannot be father of himself. It is not symmetric: x is a father of y but y cannot be the father of x.
It is not transitive: x is a father of y and y is a father of z then x cannot be the father of z.

Ex 1.1 Class 12 Maths Question 2.
Show that the relation R in the set R of real numbers, defined as
R = {(a, b) : a ≤, b²} is neither reflexive nor symmetric nor transitive.
Solution:
(i) R is not reflexive, a is not less than or equal to a² for all a ∈ R, e.g., 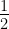 is not less than .
(ii) R is not symmetric since if a ≤ b² then b is not less than or equal to a² e.g. 2 < 5² but 5 is not less than 2².
(iii) R is not transitive: If a ≤ b², b ≤ c², then a is not less than c², e.g. 2 < (-2)², -2 < (-1)², but 2 is not less than (-1)².

Ex 1.1 Class 12 Maths Question 3.
Check whether the relation R defined in the set {1,2,3,4,5,6} as
R={(a, b): b = a+1} is reflexive, symmetric or transitive.
Solution:
(i) R is not reflexive a ≠ a + 1.
(ii) R is not symmetric if b = a + 1, then a ≠ b+ 1
(iii) R is not transitive if b = a + 1, c = b + 1 then c ≠ a + 1.

Ex 1.1 Class 12 Maths Question 4.
Show that the relation R in R defined as R={(a, b): a ≤ b}, is reflexive and transitive but not symmetric.
R = {(a,b):a≤b}
Solution:
(i) R is reflexive, replacing b by a, a ≤ a =>a = a is true.
(ii) R is not symmetric, a ≤ b, and b ≤ a which is not true 2 < 3, but 3 is not less than 2.
(iii) R is transitive, if a ≤ b and b ≤ c, then a ≤ c, e.g. 2 < 3, 3 < 4 => 2 < 4.

Ex 1.1 Class 12 Maths Question 5.
Check whether the relation R in R defined by R = {(a, b): a ≤ b³} is reflexive, symmetric or transitive.
Solution:
(i) R is not reflexive.
(ii) R is not symmetric.
(iii) R is not transitive.

Ex 1.1 Class 12 Maths Question 6.
Show that the relation R in the set {1,2,3} given by R = {(1, 2), (2,1)} is symmetric but neither reflexive nor transitive.
Solution:
(i) (1, 1),(2, 2),(3, 3) do not belong to relation R
∴ R is not reflexive.
(ii) It is symmetric (1,2) and (2,1) belong to R.
(iii) there are only two element 1 and 2 in this relation and there is no third element c in it =>R is not transitive

Ex 1.1 Class 12 Maths Question 7.
Show that the relation R in the set A of all the books in a library of a college, given by R= {(x, y): x and y have same number of pages} is an equivalence relation.
Solution:
(i) The number of pages in a book remain the same
=> Relation R is reflexive.
(ii) The book x has the same number of pages as the book y.
=> Book y has the same number of pages as the book x.
=> The relation R is symmetric.
(iii) Book x and y have the same number of pages. Also book y and z have the same number of pages.
=> Books x and z also have the same number of pages.
R is transitive also Thus, R is an equivalence relation.

Ex 1.1 Class 12 Maths Question 8.
Show that the relation R in the set A= {1,2,3,4,5} given by R = {(a, b) : |a – b| is even}, is an equivalence relation. Show that all the elements of {1,3,5} are related to each other and all the elements of {2,4} are related to each other. But no element of {1,3,5} is related to any element of {2,4}.
Solution:
A= {1,2,3,4,5} and R= {(a,b): |a – b| is even}
R= {(1,3), (1,5), (3,5), (2,4)}
(a) (i) Let us take any element of a set A. then |a – a| = 0 which is even.
=> R is reflexive.
(ii) If |a – b| is even, then |b – a| is also even, where,
R = {(a, b) : |a – b| is even} => R is symmetric.
(iii) Further a – c = a – b + b – c
If |a – b| and |b – c| are even, then their sum |a – b + b – c| is also even.
=> |a – c| is even,
∴ R is transitive. Hence R is an equivalence relation.

(b) Elements of {1,3,5} are related to each other.
Since|1 – 3| = 2, |3 – 5| = 2, |1 – 5| = 4. All are even numbers.
= Elements of {1, 3, 5} are related to each other. Similarly elements of {2,4} are related to each other. Since |2 – 4| = 2 an even number.
No element of set {1, 3, 5} is related to any element of {2,4}.

Ex 1.1 Class 12 Maths Question 9.
Show that each of the relation R in the set A = {x ∈ Z: 0 ≤ x ≤ 12}, given by
(i) R={(a,b) : |a – b|is a multiple of 4}
(ii) R={(a, b) : a = b}
is an equivalence relation. Find the set of all elements related to 1 in each case.
Solution:
The set A ∴ {x ∈ Z : 0 ≤ x ≤ 12} = {0, 1, 2,…..12}
(i) R= {(a, b): |a – b| is a multiple of 4}
|a – b| = 4k on b = a + 4k.
∴R ={(1,5),(1,9),(2, 6), (2, 10), (3, 7), (3, 11) , (4,8), (4,12), (5,9), (6,10), (7,11), (8.12) ,(0,0),(1,1), (2,2),…..(12,12)
(a) (a – a) = 0 = 4k,where k = 0=>(a,a)∈R
∴ R is reflexive.
(b) If |a – b| = 4k,then|b – a| = 4k i.e. (a,b) and (b, a) both belong to R. R is symmetric.
(c) a – c = a – b + b – c
when a – b and b – c are both multiples of 4 then a – c is also a multiple of 4. This shows if (a,b)(b,c) ∈ R then a – c also ∈ R
∴ R is an equivalence relation. The sets related 1 are {(1,5), (1,9)}.

(ii) R= {(a, b):a = b}
{(0,0), (1,1), (2,2)…..(12,12)}
(a) a = a => (a, a) ∈R
R is reflexive.
(b) Again if (a, b) ∈R, then (b, a) also ∈R
Since a = b and (a, b) ∈ R => R is symmetric.
(c) If(a, b) ∈R,then (b, c) ∈R =>a = b = c
∴ a = c => (a, c) ∈R, Hence, R is transitive set related is {1}.

Ex 1.1 Class 12 Maths Question 10.
Give an example of a relation which is
(i) Symmetric but neither reflexive nor transitive.
(ii) Transitive but neither reflexive nor symmetric.
(iii) Reflexive and symmetric but not transitive.
(iv) Reflexive and transitive but not symmetric.
(v) Symmetric and transitive but not reflexive.
Solution:
Let A = set of straight lines in a plane
(i) R: {(a, b): a is perpendicular to b} let a, b be two perpendicular lines.

(ii) Let A = set of real numbers R= {(a,b):a>b}
(a) An element is not greater than itself
∴R is not reflexive.
(b) If a > b than b is not greater than a => R is not symmetric
(c) If a > b also b > c, then a > c thus R is transitive
Hence, R is transitive but neither reflexive nor symmetric.

(iii) The relation R in the set {1,2,3} is given by R= {(a, b) :a + b≤4}
R= {(1,1), (1,2), (2,1), (1,3), (3,1), (2,2)} (1,1), (2,2) ∈ R => R is reflexive
(1,2), (2,1), (1,3), (3,1) => R is symmetric
But it is not transitive, since (2,1) ∈R, (1,3) ∈R but (2,3)∉R.

(iv) The relation R in the set {1,2,3} given by R = {(a, b): a≤b} = {(1,2), (2,2), (3,3), (2,3), 0,3)}
(a) (1,1), (2,2), (3,3) ≤R => R is reflexive
(b) (1, 2) ∈R, but (2, 1) ∉R => R is not symmetric
(c) (1,2) ∈R, (2,3) ∈R,Also (1,3) ∈R=>R is transitive.

(v) The relation R in the set {1,2,3} given by R= {(a, b): 0 < |a – b| ≤ 2} = {(1,2), (2,1), (1, 3), (3,1), (2,3), (3,2)}
(a) R is not reflexive
∵ (1,1),(2,2), (3,3) do not belong to R
(b) R is symmetric
∵ (1,2), (2,1), (1,3), (3,1), (2,3), (3,2) ∈R
(c) R is transitive (1,2) ∈R, (2,3) ∈R, Also (1,3) ∈R

Ex 1.1 Class 12 Maths Question 11.
Show that the relation R in the set A of punts in a plane given by R = {(P, Q) : distance of the point P from the origin is same as the distance of the punt Q from the origin}, is an equivalence relation. Further, show that the set of all punts related to a point P ≠ (0,0) is the circle passing through P with origin as centre.
Solution:
Let O be the origin then the relation
R={(P,Q):OP=OQ}
(i) R is reflexive. Take any distance OP,
OP = OP => R is reflexive.
(ii) R is symmetric, if OP = OQ then OQ = OP
(iii) R is transitive, let OP = OQ and OQ = OR =>OP=OR
Hence, R is an equivalence relation.
Since OP = K (constant) => P lies on a circle with centre at the origin.

Ex 1.1 Class 12 Maths Question 12.
Show that the relation R defined in the set A of all triangles as R= {(T1, T2): T1 is similar to T2}, is equivalence relation. Consider three right angle triangles T1 with sides 3,4,5, T2 with sides 5,12,13 and T3 with sides 6,8,10. Which triangles among T1, T2 and T3 are related?
Solution:
(i) In a set of triangles R = {(T1, T2) : T1 is similar T2}
(a) Since A triangle T is similar to itself. Therefore (T, T) ∈ R for all T ∈ A.
∴ Since R is reflexive
(b) If triangle T1 is similar to triangle T2 then T2 is similar triangle T1
∴ R is symmetric.
(c) Let T1 is similar to triangle T2 and T2 to T3 then triangle T1 is similar to triangle T3,
∴ R is transitive.
Hence, R is an equivalence relation.
(ii) Two triangles are similar if their sides are proportional now sides 3,4,5 of triangle T1 are proportional to the sides 6, 8, 10 of triangle T3.
∴ T1 is related to T3.

Ex 1.1 Class 12 Maths Question 13.
Show that the relation R defined in the set A of all polygons as R = {(P1, P2) : P1 and P2 have same number of sides}, is an equivalence relation. What is the set of all elements in A related to the right angle triangle T with sides 3,4 and 5?
Solution:
Let n be the number of sides of polygon P1.
R= {(P1, P2): P1 and P2 are n sides polygons}
(i) (a) Any polygon P1 has n sides => R is reflexive
(b) If P1 has n sides, P2 also has n sides then if P2 has n sides P1 also has n sides.
=> R is symmetric.
(c) Let P1, P2; P2, P3 are n sided polygons. P1 and P3 are also n sided polygons.
=> R is transitive. Hence R is an equivalence relation.
(ii) The set A = set of all the triangles in a plane.

Ex 1.1 Class 12 Maths Question 14.
Let L be the set of all lines in XY plane and R be the relation in L defined as R={(L1, L2): L1 is parallel to L2}. Show that R is an equivalence relation. Find the set of all lines related to the line y = 2x+4.
Solution:
L = set of all the lines in XY plane, R= {(L1,L2) : L1 is parallel to L2}
(i) (a) L1 is parallel to itself => R is reflexive.
(b) L1 is parallel to L2 => L2 is parallel to L1 R is symmetric.
(c) Let L1 is parallel to L2 and L2 is parallel to L3 and L1 is parallel to L3 => R is transitive.
Hence, R is an equivalence relation.
(ii) Set of parallel lines related to y = 2x + 4 is y = 2x + c, where c is an arbitrary constant.

Ex 1.1 Class 12 Maths Question 15.
Let R be the relation in the set {1,2,3,4} given by R={(1,2), (2,2), (1,1), (4,4), (1,3), (3,3), (3,2) }. Choose the correct answer.
(a) R is reflexive and symmetric but not transitive.
(b) R is reflexive and transitive but not symmetric.
(c) R is symmetric and transitive but not reflexive.
(d) R is an equivalence relation.
Solution:
(b)

Ex 1.1 Class 12 Maths Question 16.
Let R be the relation in the set N given by R = {(a, b): a=b – 2, b > 6}. Choose the correct answer.
(a)(2,4)∈R
(b)(3,8)∈R
(c)(6,8)∈R
(d)(8,7)∈R
Solution:
Option (c) satisfies the condition that a = b – 2
i. e. 6 = 8 – 2 and b > 6, i.e. b = 8
=> option (c) is correct.

Ex 1.2 Class 12 Maths Question 1.
Show that the function f: R —> R defined by f (x) =  is one-one onto, where R is the set of all non-zero real numbers. Is the result true, if the domain R is replaced by N with co-domain being same as R ?
Solution:
(a) We observe the following properties of f:
(i) f(x) =  if f(x₁) = f(x₂)

=> x₁ = x₂
Each x ∈ R has a unique image in codomain
=> f is one-one.
(ii) For each y belonging codomain then
 or  there is a unique pre image of y.
=> f is onto.

(b) When domain R is replaced by N. codomain remaining the same, then f: N—> R If f(x₁) = f(x₂)
=>  => n1 = n2 where n1; n2 ∈ N
=> f is one-one.
But for every real number belonging to codomain may not have a pre-image in N.
eg:
∴ f is not onto.

Ex 1.2 Class 12 Maths Question 2.
Check the injectivity and surjectivity of the following functions:
(i) f: N -> N given by f (x) = x²
(ii) f: Z -> Z given by f (x) = x²
(iii) f: R -> R given by f (x) = x²
(iv) f: N -> N given by f (x) = x³
(v) f: Z ->Z given by f (x) = x³
Solution:
(i) f: N —> N given by f (x) = x²
(a) f(x₁) =>f(x₂)
=>x₁² = x₂² =>x₁ = x₂
∴ f is one-one i.e. it is injective.
(b) There are such member of codomain which have no image in domain N.
e.g. 3 ∈ codomain N. But there is no pre-image in domain of f.
=> f is not onto i.e. not surjective.
(ii) f: z —> z given by f(x) = x²
(a) f (-1) = f (1) = 1 => -1 and 1 have the same image.
∴ f is not one-one i.e. not injective.
(b) There are many such elements belonging to codomain have no pre-image in its codomain z.
e.g. 3 ∈ codomain z but √3 ∉ domain z of f,
∴ f is not onto i.e. not surjective
(iii) f: R->R, given by f(x) = x²
(a) f is not one-one since f(-1) = f(1) = 1
– 1 and 1 have the same image i.e., f is not injective
(b) – 2∈ codomain R off but √-2 does not belong to domain R of f.
=> f is not onto i.e. f is not surjective.
(iv) Injective but not surjective.
(v) Injective but not surjective.

Ex 1.2 Class 12 Maths Question 3.
Prove that the Greatest Integer Function f: R->R given by f (x)=[x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.
Solution:
f: R—> R given by f (x) = [x]
(a) f(1. 2) = 1, f(1. 5) = 1 => f is not one-one
(b) All the images of x e R belonging to its domain have integers as the images in codomain. But no fraction proper or improper belonging to codomain of f has any pre-image in its domain.
=> f is not onto.

Ex 1.2 Class 12 Maths Question 4.
Show that the Modulus Function f: R -> R given by f (x) = |x|, is neither one-one nor onto, where |x| is x, if x is positive or 0 and |x| is- x, if xis negative.
Solution:
f: R->R given by f(x) = |x|
(a) f(-1) = |-1| = 1,f(1) = |1| = 1
=> -1 and 1 have the same image
∴ f is not one-one
(b) No negative value belonging to codomain of f has any pre-image in its domain
∴ f is not onto. Hence, f is neither one-one nor onto.

Ex 1.2 Class 12 Maths Question 5.
Show that the Signum Function f: R–>R given by
f(x) = 1, if x > 0
f(x) = 0, if x = 0
f(x) = – 1, if x < 0
is neither one-one nor onto.
Solution:
f: R–>R given by
f(x) = 1, if x > 0
f(x) = 0, if x = 0
f(x) = -1, if x < 0
(a) f(x₁) = f(x₂) = 1
∴ 1 and 2 have the same image i.e.
f(x₁) = f(x₂) = 1 for x>0
=> x₁≠x₂
Similarly f(x₁) = f(x₂) = – 1, for x<0 where x₁ ≠ x₂ => f is not one-one.
(b) Except – 1,0,1 no other member of codomain of f has any pre-image in its domain.
∴ f is not onto.
=> f is neither into nor onto.

Ex 1.2 Class 12 Maths Question 6.
Let A= {1,2,3}, B = {4,5,6,7} and let f = {(1,4), (2,5), (3,6)} be a function from A to B. Show that f is one-one.
Solution:
A= {1,2,3},B= {4,5,6,7} f= {(1,4), (2,5), (3,6) }.
Every member of A has a unique image in B

∴ f is one – one.

Ex 1.2 Class 12 Maths Question 7.
In each of die following cases, state whether the function is one-one, onto or bijective. Justify your answer.
(i) f: R–>R defined by f(x) = 3 – 4x
(ii) f: R–>R defined by f(x) = 1 + x²
Solution:
(i) f: R —> R defined by 3 – 4x,
f (x₁) = 3 – 4x₁, f(x₂) = 3 – 4x₂
(a) f(x₁) = f(x₂) =>3 – 4x₁ = 3 – 4x₂
=> x₁ = x₂. This shows that f is one-one
(b) f(x) = y = 3 – 4x

For every value of y belonging to its codomain. There is a pre-image in its domain => f is onto.
Hence, f is one-one onto

(ii) f: R—>R given by f(x)= 1 + x²
(a) f(1) = 1 + 1 = 2,f(-1) = 1 +1 = 2
∴ f (-1) = f (1) = 2 i.e.-1 and 1 have the same image 2.
=> f is not one-one.
(b) No negative number belonging to its codomain has its pre-image in its domain
=> f is not onto. Thus f is neither one- one nor onto.

Ex 1.2 Class 12 Maths Question 8.
Let A and B be sets. Show that f:A x B –>B x A such that f (a, b) = (b, a) is bijective function.
Solution:
We have f: (A x B) —> B x A such that f (a, b) = b, a
(a) ∴ f(a1, b1)= (b1, a1) f(a2, b2) = (b2, a2) f(a1, b1) = f(a2, b2)
=>(b1, a1)
= (b2, a2)
=> b1 = b2 and a1 = a2 f is one-one
(b) Every member (p, q) belonging to its codomain has its pre-image in its domain as (q, p) f is onto. Thus, f is one-one and onto i.e. it is bijective.

Ex 1.2 Class 12 Maths Question 9.
Let f: N —> N be defined by
f (n) =  ,if n is odd
f (n) =  ,if n is even
for all n∈N
State whether the function f is bijective. Justify your answer.
Solution:
f: N —> N, defined by

The elements 1, 2 belonging to domain of f have the same image 1 in its codomain
=> f is not one-one.
∴ it is not injective,
(b) Every member of codomain has pre-image in its domain e.g. 1 has two pre-images 1 and 2
=> f is onto. Thus f is not one-one but it is onto
=> f is not bijective.

Ex 1.2 Class 12 Maths Question 10.
Let A = R-{3} and B = R-{1}. consider the function f: A -> B defined by f (x) = 
Solution:
Is f one-one and onto? Justify your answer.
f: A –> B where A = R – {3}, B = R – {1} f is defined by

Ex 1.2 Class 12 Maths Question 11.
Let f: R -> R be defined as f (x)=x⁴. Choose the correct answer.
(a) f is one-one onto
(b) f is many-one onto
(c) f is one-one but not onto
(d) f is neither one-one nor onto
Solution:
f(-1) = (-1)⁴ = 1,f(1) = 1⁴ = 1
∴ – 1, 1 have the same image 1 => f is not one- one
Further – 2 in the codomain of f has no pre-image in its domain.
∴ f is not onto i.e. f is neither one-one nor onto Option (d) is correct.

Question 12.
Let f: R –> R be defined as f (x)=3x. Choose the correct answer.
(a) f is one-one onto
(b) f is many-one onto
(c) f is one-one but not onto
(d) f is neither one-one nor onto
Solution:
f: R –> R is defined by f (x) = 3x
(a) f(x₁) = 3x₁, f(x₂) = 3x₂
=> f(x₁) = f(x₂)
=> 3x₁ = 3x₂
=> x₁ = x₂
=> f is one-one
(b) for every member y belonging to co-domain has pre-image x in domain of f.
∵ y = 3x
=>
f is onto
f is one-one and onto. Option (a) is correct.

Ex 1.3 Class 12 Maths Question 1.
Let f: {1,3,4} –> {1,2, 5} and g : {1, 2,5} –> {1,3} be given by f = {(1, 2), (3,5), (4,1) and g = {(1,3), (2,3), (5,1)}. Write down g of.
Solution:
f= {(1,2),(3,5),(4,1)}
g= {(1,3),(2,3),(5,1)}
f(1) = 2, g(2) = 3 => gof(1) = 3
f(3) = 5, g(5)= 1 =>gof(3) = 1
f(4) = 1, g(1) = 3 => gof(4) = 3
=> gof= {(1,3), (3,1), (4,3)}

Ex 1.3 Class 12 Maths Question 2.
Let f, g and h be functions from R to R. Show that (f + g) oh = foh + goh, (f • g) oh = (foh) • (goh)
Solution:
f + R –> R, g: R –> R, h: R –> R
(i) (f+g)oh(x)=(f+g)[h(x)]
= f[h(x)]+g[h(x)]
={foh} (x)+ {goh} (x)
=>(f + g) oh = foh + goh
(ii) (f • g) oh (x) = (f • g) [h (x)]
= f[h (x)] • g [h (x)]
= {foh} (x) • {goh} (x)
=> (f • g) oh = (foh) • (goh)

Ex 1.3 Class 12 Maths Question 3.
Find gof and fog, if
(i) f (x) = |x| and g (x) = |5x – 2|
(ii) f (x) = 8x³ and g (x) = .
Solution:
(i) f(x) = |x|, g(x) = |5x – 2|
(a) gof(x) = g(f(x)) = g|x|= |5| x | – 2|
(b) fog(x) = f(g (x)) = f(|5x – 2|) = ||5 x – 2|| = |5x-2|
(ii) f(x) = 8x³ and g(x) = 
(a) gof(x) = g(f(x)) = g(8x³) =  = 2x
(b) fog (x) = f(g (x))=f() = 8.()³ = 8x

Ex 1.3 Class 12 Maths Question 4.
If , show that fof (x) = x, for all . What is the inverse of f?
Solution:

(a) fof (x) = f(f(x)) = 

Ex 1.3 Class 12 Maths Question 5.
State with reason whether following functions have inverse
(i) f: {1,2,3,4}–>{10} with f = {(1,10), (2,10), (3,10), (4,10)}
(ii) g: {5,6,7,8}–>{1,2,3,4} with g = {(5,4), (6,3), (7,4), (8,2)}
(iii) h: {1,2,3,4,5}–>{7,9,11,13} with h = {(2,7), (3,9), (4,11), (5,13)}
Solution:
f: {1,2,3,4} –> {10} with f = {(1,10), (2,10), (3,10), (4,10)}
(i) f is not one-one since 1,2,3,4 have the same image 4.
=> f has no inverse.
(ii) g: {5,6,7,8} –> {1,2,3,4} with g = {(5,4), (6,3) , (7,4), (8,2)}
Here also 5 and 7 have the same image
∴ g is not one-one. Therefore g is not invertible.
(iii) f has an inverse

Ex 1.3 Class 12 Maths Question 6.
Show that f: [-1,1] –> R, given by f(x) =  is one-one. Find the inverse of the function f: [-1,1] –> Range f.
Hint – For y ∈ Range f, y = f (x) =  for some x in [- 1,1], i.e., x = 
Solution:
Ex 1.3 Class 12 Maths Question 7.
Consider f: R –> R given by f (x) = 4x + 3. Show that f is invertible. Find the inverse of f.
Solution:
f: R—>R given by f(x) = 4x + 3
f (x₁) = 4x₁ + 3, f (x₂) = 4x₂ + 3
If f(x₁) = f(x₂), then 4x₁ + 3 = 4x₂ + 3
or 4x₁ = 4x₂ or x₁ = x₂
f is one-one
Also let y = 4x + 3, or 4x = y – 3
∴ 
For each value of y ∈ R and belonging to co-domain of y has a pre-image in its domain.
∴ f is onto i.e. f is one-one and onto
f is invertible and f^-1 (y) = g (y) = 

Ex 1.3 Class 12 Maths Question 8.
Consider f: R₊ –> [4, ∞] given by f (x) = x² + 4. Show that f is invertible with the inverse f^-1 of f given by f^-1 (y) = √y-4 , where R₊ is the set of all non-negative real numbers.
Solution:
f(x₁) = x₁² + 4 and f(x₂) = x₂² + 4
f(x₁) = f(x₂) => x₁² + 4 = x₂² + 4
or x₁² = x₂² => x₁ = x₂ As x ∈ R
∴ x>0, x₁² = x₂² => x₁ = x₂ =>f is one-one
Let y = x² + 4 or x² = y – 4 or x = ±√y-4
x being > 0, -ve sign not to be taken
x = √y – 4
∴ f^-1 (y) = g(y) = √y-4 ,y ≥ 4
For every y ≥ 4, g (y) has real positive value.
∴ The inverse of f is f^-1 (y) = √y-4

Ex 1.3 Class 12 Maths Question 9.
Consider f: R₊ –> [- 5, ∞) given by f (x) = 9x² + 6x – 5. Show that f is invertible with

Solution:
Let y be an arbitrary element in range of f.
Let y = 9x² + 6x – 5 = 9x² + 6x + 1 – 6
=> y = (3x + 1)² – 6
=> y + 6 = (3x + 1)²
=> 3x + 1 = √y + 6

Ex 1.3 Class 12 Maths Question 10.
Let f: X –> Y be an invertible function. Show that f has unique inverse.
Hint – suppose g₁ and g₂ are two inverses of f. Then for all y∈Y, fog₁(y)=I_y(y)=fog₂(y).Use one-one ness of f.
Solution:
If f is invertible gof (x) = I_x and fog (y) = I_y
∴ f is one-one and onto.
Let there be two inverse g₁ and g₂
fog₁ (y) = I_y, fog₂ (y) = I_y
I_y being unique for a given function f
=> g₁ (y) = g₂ (y)
f is one-one and onto
f has a unique inverse.

Ex 1.3 Class 12 Maths Question 11.
Consider f: {1,2,3} –> {a, b, c} given by f (1) = a, f (2)=b and f (3)=c. Find f^-1 and show that (f^-1)f^-1=f.
Solution:
f: {1,2, 3,} –> {a,b,c} so that f(1) = a, f(2) = b, f(3) = c
Now let X = {1,2,3}, Y = {a,b,c}
∴ f: X –> Y
∴ f^-1: Y –> X such that f^-1 (a)= 1, f^-1(b) = 2; f^-1(c) = 3
Inverse of this function may be written as
(f^-1)^-1 : X –> Y such that
(f^-1)^-1 (1) = a, (f^-1)^-1 (2) = b, (f^-1)^-1 (3) = c
We also have f: X –> Y such that
f(1) = a,f(2) = b,f(3) = c => (f^-1)^-1 = f

Ex 1.3 Class 12 Maths Question 12.
Let f: X –> Y be an invertible function. Show that the inverse of f^-1 is f, i.e., (f^-1)^-1 = f.
Solution:
f: X —> Y is an invertible function
f is one-one and onto
=> g : Y –> X, where g is also one-one and onto such that
gof (x) = I_x and fog (y) = I_y => g = f^-1
Now f^-1 o (f^-1)^-1 = I
and fo[f^-1o (f^-1)^-1] =fol
or (fof^-1)^-1 o (f^-1)^-1 = f
=> Io (f^-1)^-1 = f
=> (f^-1)^-1 = f

Ex 1.3 Class 12 Maths Question 13.
If f: R –> R be given by f(x) = , then fof (x) is
(a) 
(b) x³
(c) x
(d) (3 – x³)
Solution:
f: R-> R defined by f(x) = 
fof (x) = f[f(x)] = 
= 
= 
= 
= x

Ex 1.3 Class 12 Maths Question 14.
Let f:  be a function defined as f (x) =  . The inverse of f is the map g: Range f–>  given by
(a) 
(b) 
(c) 
(d) 
Solution:
(b)

Ex 1.4 Class 12 Maths Question 1.
Determine whether or not each of the definition of * given below gives a binary operation. In the event that * is not a binary operation, give justification for this.
(i) On Z⁺,define * by a * b = a – b
(ii) On Z⁺, define * by a * b = ab
(iii) On R, define * by a * b = ab²
(iv) On Z⁺,define * by a * b = |a – b|
(v) On Z⁺, define * by a * b = a
Solution:
(i) If a > b, a * b = a – b > 0, which belongs to Z⁺.
But if a < b, a * b = a – b < 0, which does not belong to Z⁺
=> * given operation is not a binary operation.
(ii) For all a and b belonging to Z^-1, ab also belongs to Z⁺.
∴ The operation *, defined by a * b = ab is a binary operation.
(iii) For all a and b belonging to R, ab² also belongs to R.
∴ The operation * defined by a * b = ab² is binary operation.
(iv) For all a and b belonging to Z⁺, |a – b| also belongs to Z⁺¹
∴ The operation a * b = |a – b| is a binary operation.
(v) On Z⁺ defined by a * b = a
a, b ∈ Z⁺ = a ∈ Z⁺
∴ The operation * is a binary operation.

Ex 1.4 Class 12 Maths Question 2.
For each binary operation * defined below, determine whether * is commutative or associative.
(i) OnZ, define a * b = a – b
(ii) OnQ, define a * b = ab + 1
(iii) On Q, define a * b = 
(iv) On Z⁺, define a * b = 2ab
(v) On Z⁺, define a * b = ab
(vi) On R- {-1}, define a * b = 
Solution:
(i) On Z, operation * is defined as
(a) a * b = a – b => b * a = b – a
But a – b ≠ b – a ==> a * b ≠ b * a
Defined operation is not commutative
(b) a – (b – c) ≠ (a – b) – c
Binary operation * as defined is not associative.

(ii) On Q, Operation * is defined as a * b = ab + 1
(a) ab + 1 = ba + 1, a * b = b * a
Defined binary operation is commutative.
(b) (a*b)*c = (ab + 1)*c = (ab + 1)c + 1 = abc + c + 1
a * (b * c) = a * (bc + 1) = a(bc + 1)+ 1 = abc + a+ 1
=> a * (b * c) ≠ (a * b) * c
∴ Binary operation defined is not associative.

(iii) (a) On Q, operation * is defined as a * b = 
∴ a * b = b * a
∴ Operation binary defined is commutative.
be abc
(b) a * (b * c) = a *  =  and
(a * b) * c =  * c 
=> (a * b) * c =  * c 
Defined binary operation is associative.

(iv) On Z⁺ operation * is defined as a * b = 2^ab
(a) a * b = 2^ab, b * a = 2^ba = 2^ab
=> a * b = b * a .
∴ Binary operation defined as commutative.
(b) a * (b * c) = a * 2^ba = 2^a.2bc
(a * b) * c = 2^ab * c = 2^2ab
Thus (a * b) * c ≠ a * (b * c)
∴ Binary operation * as defined as is not associative.

(v) On Z⁺, a * b = ab
(a) b * a = b^a .
∴ a^b ≠ b^a = a * b ≠ b * a.
* is not commutative.
(b) (a*b)*c = a^b*c = (a^b)^c = a^bc a*(b* c)
= a*b^c = a^bc
Thus (a * b) * c ≠ (a * b * c)
∴ Operation * is not associative.

(vi) Neither commutative nor associative.

Ex 1.4 Class 12 Maths Question 3.
Consider the binary operation ^ on the set {1, 2, 3, 4, 5} defined by a ^ b=min {a, b}. Write the operation table of the operation ^.
Solution:
Operation ^ table on the set {1, 2, 3, 4, 5} is as follows.

Ex 1.4 Class 12 Maths Question 4.
Consider a binary operation * on the set {1, 2, 3, 4, 5} given by the following multiplication table.
(i) Compute (2 * 3) * 4 and 2 * (3 * 4)
(ii) Is * commutative?
(iii) Compute (2 * 3) * (4 * 5).
Hint – use the following table)

Solution:
(i) From the given table, we find
2*3 = 1, 1*4 = 1
(a) (2*3)*4 = 1 * 4 = 1
(b) 2*(3*4) = 2 * 1 = 1
(ii) Let a, b ∈ {1,2,3,4,5} From the given table, we find
a*a = a
a*b = b*a = 1 when a or b or are odd and a b.
2 * 4 = 4 * 2 = 2, when a and b are even and a ≠ b
Thus a * b = b * c
∴Binary operation * given is commutative.
(iii) Binary operation * given is commutative (2 * 3) * (4 * 5) = 1 * 1 = 1.

Ex 1.4 Class 12 Maths Question 5.
Let *’ be the binary operation on the set {1,2,3,4,5} defined by a *’ b=H.C.F. of a and b. Is the operation *’ same as the operation * defined in the exp no. 4 above? Justify your answer.
Solution:
The set is {1,2,3,4, 5} and a * b = HCF of a and b.
Let us prepare the table of operation *.

Ex 1.4 Class 12 Maths Question 6.
Let * be the binary operation on N given by a * b = L.C.M. of a and b.Find
(i) 5 * 7, 20 * 16
(ii) Is * commutative?
(iii) Is * associative?
(iv) Find the identity of * in N
Solution:
Binary operation * defined as a * b = 1 cm. of a and b.
(i) 5 * 7 = 1 cm of 5 and 7 = 35
20 * 16= 1 cm of 20 and 16 = 80
(ii) a * b= 1 cm of a and b b * a = 1 cm of b and a
=> a * b = b * a, 1 cm of a, b and b, a are equal
∴ Binary operation * is commutative.
(iii) a * (b * c) = 1 cm of a, b, c and (a * b) * c = 1 cm of a, b, c
=> a * (b * c) = (a * b) * c
=> Binary operation * given is associative.
(iv) Identity of * in N is 1
1 * a = a * 1 = a = 1 cm of 1 and a.
(v) Let * : N x N—> N defined as a * b = 1.com of (a, b)
For a = 1, b = 1, a * b = l b * a
Otherwise a * b ≠ 1
∴ Binary operation * is not invertible
=> 1 is invertible for operation *

Ex 1.4 Class 12 Maths Question 7.
Is * defined on the set {1, 2, 3, 4, 5} by a * b = L.C.M. of a and b a binary operation? Justify your answer.
Solution:
The given set = {1,2,3,4,5} Binary operation is defined as a * b = 1 cm of a and b. 4 * 5 = 20 which does not belong to the given set {1, 2, 3, 4, 5}.
It is not a binary operation.

Ex 1.4 Class 12 Maths Question 8.
Let * be the binary operation on N defined by a * b = H.C.F. of a and b. Is * commutative? Is * associative? Does there exist identity for this binary operation on N?
Solution:
Binary operation on set N is defined as a * b = HCF of a and b
(a) We know HCF of a, b = HCF of b, a
∴ a * b = b * a
∴ Binary operation * is commutative.
(b) a*(b*c) = a* (HCF of b, c) = HCF of a and (HCF of b, c) = HCF of a, b and c
Similarly (a * b) * c = HCF of a, b, and c
=> (a * b) * c = a * (b * c)
Binary operation * as defined above is associative.
(c) 1 * a = a * 1 = 1 ≠ a
∴ There does not exists any identity element.

Ex 1.4 Class 12 Maths Question 9.
Let * be a binary operation on the set Q of rational numbers as follows:
(i) a * b = a – b
(ii) a * b = a² + b²
(iii) a * b = a + ab
(iv) a * b = (a – b)²
(v) a * b = 
(vi) a * b = ab²
Find which of the binary operations are commutative and which are associative.
Solution:
Operation is on the set Q.,,
(i) defined as a * b = a – b
(a) Now b * a = b – a
But a – b ≠ b – a
∴ a * b ≠ b * a
∴ Operation * is not commutative.
(b) a * (b * c) = a * (b – c) = a – (b – c) = a – b + c (a * b) * c = (a – b) * c = a – b – c
Thus a * (b * c)¹ (a * b) * c = (a² + b²)² + c²
=> a * (b * c) ≠ (a * b) * c
∴ The operation * as defined is not associative.

(ii) (a) a * b = a² + b * a = b² + a² = a² + b².
a * b = b * a
This binary operation is commutative,
(b) a*(b*c) = a*(b² + c²) = a² + (b²)² + c²)²
=> (a*b)*c = (a² + b²)*c = (a² + b²) + c²
Thus a * (b*c) (a*b) * c
The operation * given is not associative.

(iii) Operation * is defined as a * b = a + ab
(a) b * a = b + ba
a * b ≠ b * a
The operation is not commutative.
(b) a*(b*c) = a*(b + bc)
= a + a(b + bc)
= a + ab + abc (a * b) * c
= (a + ab) * c
= (a + ab) + (a + ab) • c
= a + ab + ac + abc
=> a * (b * c) ≠ (a * b) * c
=> The binary operation is not associative.

(iv) The binary operation is defined as a * b = (a – b)²
(a) b*a = (b – a)² = (a – b)² => a*b = b*a
.’. This binary operation * is commutative.
(b) a*(b*c) = a*(b – c)² = [a – (b – c)²]² (a * b) * c
= (a – b)² * c
= [(a – b)² – c]²
=> a * (b * c) ≠ (a * b) * c
the operation * is not associative.

(v) Commutative and associative.

(vi) Neither commutative nor associative.

Ex 1.4 Class 12 Maths Question 10.
Show that none of the operations given above has identity.
Solution:
The binary operation * on set Q is
(i) defined as a*b = a – b
For identity element e, a*e = e*a = a
But a*e = a – e≠a and e*a = e – a≠a
There is no identity element for this operation
(ii) Binary operation * is defined as a * b = a² + b² ≠ a
This operation * has no identity.
(iii) The binary operation is defined as a*b = a+ab
Putting b = e, a + e = a + eb ≠ a
There is no identity element.
(iv) The binary operation is defined as a * b = (a – b)²
Put b = e, a * e = (a – e)² ≠ a for any value of
e∈Q
=> there is no Identity Element.
(v) The operation is a * b = 
∴ a * e =  ≠ a for any value of e ∈ Q
∴ Operation * has no identity
(vi) The operation * is a * b = ab² Put b = e, a
*e = ae² and e * a = ea² ≠ a for any value of e∈Q
=> There is no Identity Element. Thus, these operations have no Identity.

Ex 1.4 Class 12 Maths Question 11.
Let A=N x N and * be the binary operation on A defined by (a,b)*(c,d)=(a+c,b+d)
Show that * is commutative and associative. Find the identity element for * on A, if any.
Solution:
A = N x N Binary operation * is defined as (a, b) * (c, d) = (a + c, b + d)
(a) Now (c, d) * (a,b) = (c+a, d+b) = (a+c,b+d)
=> (a, b) * (c, d) = (c, d) * (a, b)
∴ This operation * is commutative
(b) Next(a,b)* [(c,d)*(e,f)]=(a,b)*(c+e,d+f) = ((a + c + e), (b + d + f))
and [(a, b) * (c, d)] * (e, f)=(a+c, b+d) * (e, f) = ((a + c + e, b+d + f))
=> (a, b) * [(c, d) * (e, f)] = [(a, b) * (c, d)] * (e,f)
∴ The binary operation given is associative
(c) Identity element does not exists.

Ex 1.4 Class 12 Maths Question 12.
State whether the following statements are true or false. Justify.
(i) For an arbitrary binary operation * on a set N,
a*a=a∀a∈N.
(ii) If * is a commutative binary operation on N, then
a * (b * c) = (c * b) * a
Solution:
(i) A binary operation on N is defined as
a*a=a∀a∈N.
Here operation * is not defined.
∴ Given statement is false.
(ii) * is a binary commutative operation on N. c
* b = b * c
∵ * is commutative
∵ (c * b) * a = (b * c) * a = a * (b * c)
∴ Thus a * (b * c) = (c * b) * a
This statement is true.

Ex 1.4 Class 12 Maths Question 13.
Consider a binary operation * on N defined as a * b = a³ + b³. Choose the correct answer.
(a) Is * both associative and commutative?
(b) Is * commutative but not associative?
(c) Is * associative but not commutative?
(d) Is * neither commutative nor associative?
Solution:
(b)